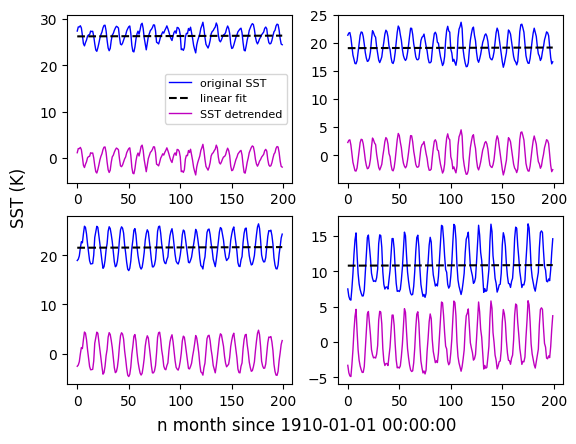
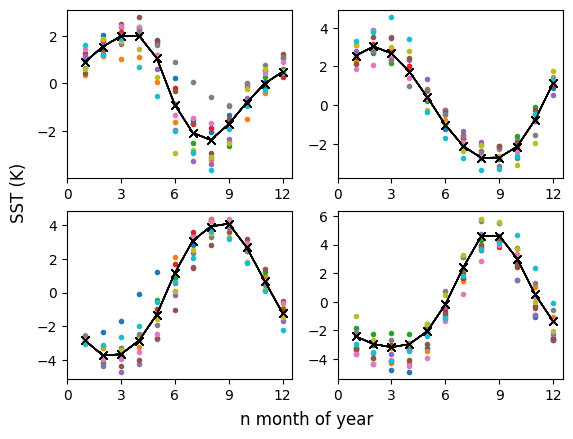
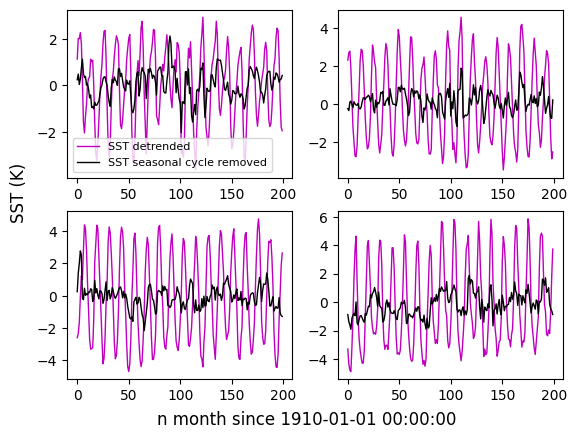
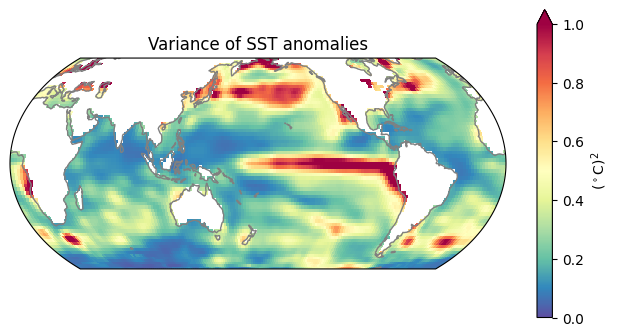
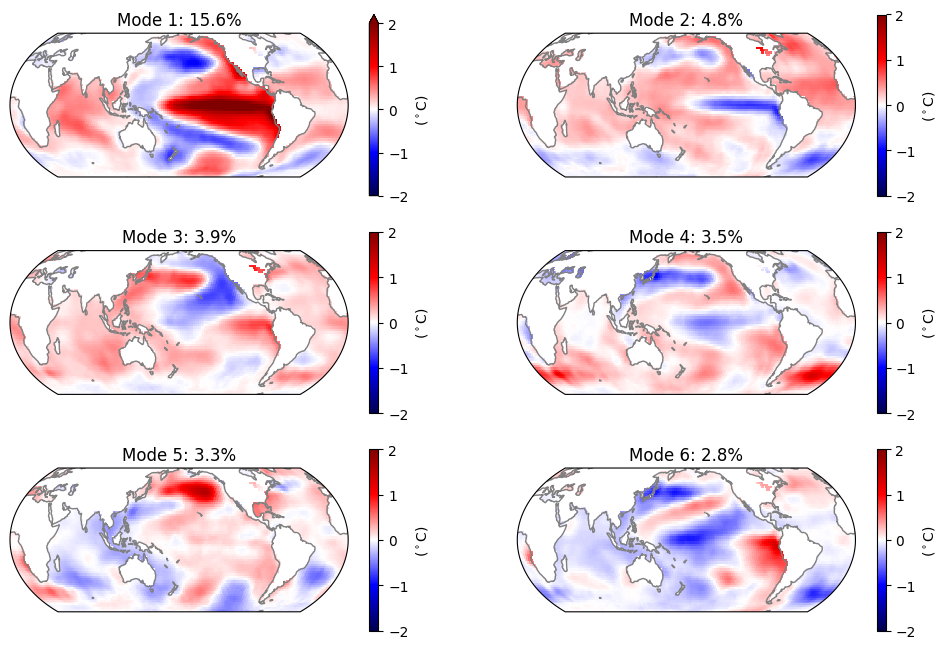
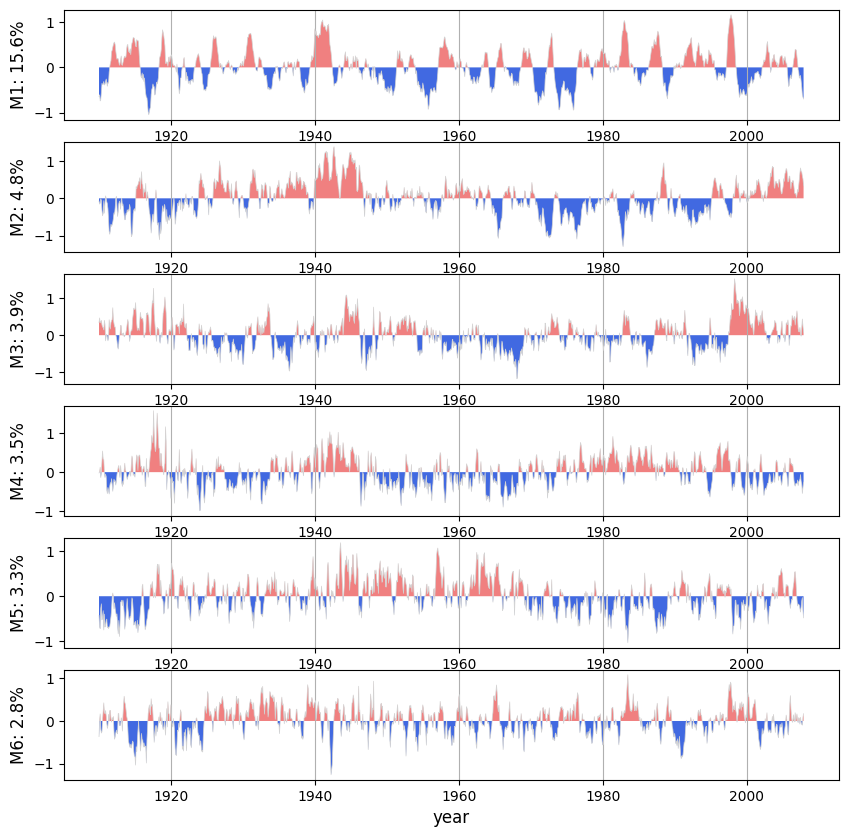
0.0 2.0 4.0 ... 354.0 356.0 358.0
array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18., 20., 22.,
24., 26., 28., 30., 32., 34., 36., 38., 40., 42., 44., 46.,
48., 50., 52., 54., 56., 58., 60., 62., 64., 66., 68., 70.,
72., 74., 76., 78., 80., 82., 84., 86., 88., 90., 92., 94.,
96., 98., 100., 102., 104., 106., 108., 110., 112., 114., 116., 118.,
120., 122., 124., 126., 128., 130., 132., 134., 136., 138., 140., 142.,
144., 146., 148., 150., 152., 154., 156., 158., 160., 162., 164., 166.,
168., 170., 172., 174., 176., 178., 180., 182., 184., 186., 188., 190.,
192., 194., 196., 198., 200., 202., 204., 206., 208., 210., 212., 214.,
216., 218., 220., 222., 224., 226., 228., 230., 232., 234., 236., 238.,
240., 242., 244., 246., 248., 250., 252., 254., 256., 258., 260., 262.,
264., 266., 268., 270., 272., 274., 276., 278., 280., 282., 284., 286.,
288., 290., 292., 294., 296., 298., 300., 302., 304., 306., 308., 310.,
312., 314., 316., 318., 320., 322., 324., 326., 328., 330., 332., 334.,
336., 338., 340., 342., 344., 346., 348., 350., 352., 354., 356., 358.])